与归并排序相关的一些问题

与归并排序相关的一些问题

作者：Grey

原文地址：

博客园：与归并排序相关的一些问题

CSDN：与归并排序相关的一些问题

归并排序的递归解法

插入，选择，冒泡排序时间复杂度是O(N^2)，归并排序可以做到时间复杂度O(N*logN)。

归并排序的整体思路是利用递归，先让左边排好序，再让右边排好序，然后通过merge操作让整体有序。

merge操作类似合并两个及以上有序链表问题中提到的算法。

但是merge过程需要辅助数组，所以额外空间复杂度为O(N)。

完整代码和注释见：

public class Code_MergeSort {    // 递归方法实现    public static void mergeSort1(int[] arr) {        if (arr == null || arr.length < 2) {            return;        }        process(arr, 0, arr.length - 1);    }    // 递归过程，让l...r变有序    public static void process(int[] arr, int l, int r) {        if (l == r) {            return;        }        // 求中点        int mid = l + ((r - l) >> 1);        // 左边部分有序        process(arr, l, mid);        // 右边部分有序        process(arr, mid + 1, r);        // 整体变有序        merge(arr, l, mid, r);    }    // arr[l...mid]已经有序    // arr[mid+1...r]也已经有序    // 将arr[l...r]整体变有序    public static void merge(int[] arr, int l, int mid, int r) {        // 辅助数组        int[] help = new int[r - l + 1];        int ls = l;        int rs = mid + 1;        int i = 0;        while (ls <= mid && rs <= r) {            // 谁小拷贝谁到辅助数组中。            if (arr[ls] < arr[rs]) {                help[i++] = arr[ls++];            } else {                help[i++] = arr[rs++];            }        }        // 左边和右边剩余部分直接拷贝到辅助数组中        while (ls <= mid) {            help[i++] = arr[ls++];        }        while (rs <= r) {            help[i++] = arr[rs++];        }        i = 0;        for (int n : help) {            arr[l + (i++)] = n;        }    }}

这个递归过程时间复杂度可以利用 master 公式来计算。

T(N) = 2*T(N/2) + O(N^1)

故上述算法时间复杂度为O(N*logN)

归并排序的迭代版本实现

因为任何递归函数都可以用非递归函数来实现，所以，归并排序有对应的迭代方法，思路如下

1. 设置一个步长，从 1 开始，1，2，4，8，16....2^n 方式递增

2. 每次处理对应步长的数组区间范围内的排序。

3. 步长超过或者等于数组长度，则整个数组排序完成。

比如[1,3,4,2,5,6,4,6,8]

先设置步长为 1，数组分成如下区间

[0...1],[2...3],[4...5],[6...7],[8...8]

注：最后一组不够分，则单独作为一组处理。

将如上区间内部排好序，得到的数组为

[1,3,2,4,5,6,4,6,8]

然后设置步长为 2，数组分成如下区间

[0...3],[4...7],[8...8]。

然后将上述区间内部先排好序，得到数组为

[1,2,3,4,4,5,6,6,8]

然后设置步长为 4，数组分成如下区间

[0...7],[8...8]。

然后将上述区间内部先排好序，得到数组为

[1,2,3,4,4,5,6,6,8]

最后设置步长为 8，数组只有一个区间，直接排序，得到最后结果

[1,2,3,4,4,5,6,6,8]

完整代码见

public class Code_MergeSort {    // 归并排序的迭代版    public static void mergeSort2(int[] arr) {        if (arr == null || arr.length < 2) {            return;        }        int len = arr.length;        // 步长，1，2，4，8....        int step = 1;        while (step < len) {            // 左组的第一个位置            int lStart = 0;            while (lStart < len) {                if (lStart + step >= len) {                    // 没有右组                    break;                }                int mid = lStart + step - 1;                // rEnd不能越界                int rEnd = mid + Math.min(step, len - mid - 1);                // 右组中第一个位置                // 中点位置                merge(arr, lStart, mid, rEnd);                lStart = rEnd + 1;            }            // 防止溢出            if (step > (len / 2)) {                break;            }            step <<= 1;        }    }    // arr[l...mid]已经有序    // arr[mid+1...r]也已经有序    // 将arr[l...r]整体变有序    public static void merge(int[] arr, int l, int mid, int r) {        // 辅助数组        int[] help = new int[r - l + 1];        int ls = l;        int rs = mid + 1;        int i = 0;        while (ls <= mid && rs <= r) {            // 谁小拷贝谁到辅助数组中。            if (arr[ls] < arr[rs]) {                help[i++] = arr[ls++];            } else {                help[i++] = arr[rs++];            }        }        // 左边和右边剩余部分直接拷贝到辅助数组中        while (ls <= mid) {            help[i++] = arr[ls++];        }        while (rs <= r) {            help[i++] = arr[rs++];        }        i = 0;        for (int n : help) {            arr[l + (i++)] = n;        }    }}

合并有序数组

题目描述见LeetCode 88. Merge Sorted Array

本题思路就是归并排序的merge过程，不赘述，代码如下

class Solution {    public void merge(int[] nums1, int m, int[] nums2, int n) {        int len = m + n;        while (m > 0 && n > 0) {            if (nums1[m - 1] > nums2[n - 1]) {                nums1[--len] = nums1[--m];            } else {                nums1[--len] = nums2[--n];            }        }        while (n > 0) {            nums1[--len] = nums2[--n];        }    }}

注：本题在 LintCode 中也有，见LintCode 6 · Merge Two Sorted Arrays

在 LintCode 中，对本题有个扩展要求：

如果一个数组很大，另一个数组很小，你将如何优化算法？

对于扩展要求，我们可以用如下方式来优化

即直接查小数组中的元素在大数组中的位置（可以用二分），然后依次填入具体位置

完整代码见

public class Solution {    public static int[] mergeSortedArray(int[] A, int[] B) {        int m = A.length;        int n = B.length;        int[] bigger = m >= n ? A : B;        int[] smaller = bigger == A ? B : A;        int[] helper = new int[m + n];        int from = 0;        int to;        int index = 0;        for (int i = 0; i < smaller.length; i++) {            int position = position(smaller[i], bigger, i);            helper[position] = smaller[i];            to = position - 1;            while (from <= to) {                helper[from++] = bigger[index++];            }            from = position + 1;        }        while (from < (m + n)) {            helper[from++] = bigger[index++];        }        return helper;    }    // value在bigger的位置是多少    public static int position(int value, int[] bigger, int offset) {        int smallerThanMe = 0;        int L = 0;        int R = bigger.length - 1;        while (L <= R) {            int mid = L + ((R - L) >> 1);            if (bigger[mid] > value) {                R = mid - 1;            } else if (bigger[mid] < value) {                smallerThanMe = (mid + 1);                L = mid + 1;            } else {                smallerThanMe = mid;                R = mid - 1;            }        }        return smallerThanMe + offset;    }}

计算右侧小于当前元素的个数问题

题目描述见：LeetCode 315. Count of Smaller Numbers After Self

本题也是利用了归并排序的merge过程，由于归并排序是从小到大排序，而我们需要得到某个元素右侧有多少比它小，所以我们还需要将归并排序改成从大到小排序。

以某一次merge过程为例，比如

左侧区间（已排好序）: [5,3,2,1]

右侧区间（已排好序）：[6,4,3,3]

示例图如下

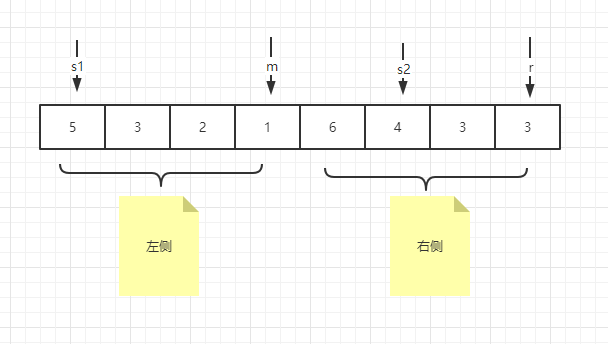
当左侧指针来到s1的时候，右侧指针移动到s2的时候，开始比左侧的值要小，此时可以结算s1位置右侧有几个比它小的元素。

左侧组中比 s1 更小的元素个数 + (r - s2 + 1)

完整代码见：

class Solution {   public static class Node {        public int value;        public int index;        public Node(int index, int value) {            this.value = value;            this.index = index;        }    }    // 思路转换为：一个数的右边有多少个数比它小！    // 改归并排序（从大到小）    public static List<Integer> countSmaller(int[] nums) {        List<Integer> result = new ArrayList<>(nums.length);        Node[] nodes = new Node[nums.length];        for (int i = 0; i < nums.length; i++) {            result.add(0);            nodes[i] = new Node(i, nums[i]);        }        process(nodes, 0, nums.length - 1, result);        return result;    }    private static void process(Node[] nodes, int l, int r, List<Integer> result) {        if (l == r) {            return;        }        int m = l + ((r - l) >> 1);        process(nodes, l, m, result);        process(nodes, m + 1, r, result);        merge(nodes, l, m, r, result);    }    private static void merge(Node[] nodes, int l, int m, int r, List<Integer> result) {        Node[] help = new Node[r - l + 1];        int s1 = l;        int s2 = m + 1;        int index = 0;        while (s1 <= m && s2 <= r) {            if (nodes[s1].value > nodes[s2].value) {                result.set(nodes[s1].index, result.get(nodes[s1].index) + r - s2 + 1);                help[index++] = nodes[s1++];            } else if (nodes[s1].value < nodes[s2].value) {                help[index++] = nodes[s2++];            } else {                help[index++] = nodes[s2++];            }        }        while (s1 <= m) {            help[index++] = nodes[s1++];        }        while (s2 <= r) {            help[index++] = nodes[s2++];        }        for (int i = 0; i < help.length; i++) {            nodes[l + i] = help[i];        }    }}

LintCode上有一个类似的题目，题目描述见：LintCode 532 · Reverse Pairs

本题的思路和上一题一致，都是先将归并排序改成从大到小排序，然后在merge过程中，求一个数右侧有几个数比它小，不赘述，代码见：

public class Solution {   public static long reversePairs(int[] A) {        if (null == A || A.length < 2) {            return 0;        }        return process(A, 0, A.length - 1);    }    private static long process(int[] a, int l, int r) {        if (l == r) {            return 0L;        }        int m = l + ((r - l) >> 1);        return process(a, l, m) + process(a, m + 1, r) + merge(a, l, m, r);    }    private static long merge(int[] a, int l, int m, int r) {        int[] help = new int[r - l + 1];        int index = 0;        int s1 = l;        int s2 = m + 1;        long ans = 0L;        while (s1 <= m && s2 <= r) {            if (a[s1] < a[s2]) {                help[index++] = a[s2++];            } else if (a[s1] > a[s2]) {                ans += (r - s2 + 1);                help[index++] = a[s1++];            } else {                help[index++] = a[s2++];            }        }        while (s1 <= m) {            help[index++] = a[s1++];        }        while (s2 <= r) {            help[index++] = a[s2++];        }        index = 0;        for (int n : help) {            a[l + (index++)] = n;        }        return ans;    }}

翻转对问题

题目描述见：LeetCode 493. Reverse Pairs

本题也是利用merge过程，不同于上述两个问题，本题在merge两个区间之前，就要先统计一下num[i] > 2 * num[j]的数量。

完整代码见：

class Solution {   public static int reversePairs(int[] A) {        if (null == A || A.length < 2) {            return 0;        }        int size = A.length;        return process(A, 0, size - 1);    }    public static int process(int[] a, int l, int r) {        if (l == r) {            return 0;        }        int m = l + ((r - l) >> 1);        return process(a, l, m) + process(a, m + 1, r) + merge(a, l, m, r);    }    public static int merge(int[] a, int l, int m, int r) {        // 先执行统计        int ans = 0;        int s1 = l;        int s2 = m + 1;        while (s1 <= m && s2 <= r) {            if ((long) a[s1] - (long) a[s2] > (long) a[s2]) {                ans += (r - s2 + 1);                s1++;            } else {                s2++;            }        }        // 以下是经典mergesort排序        int[] help = new int[r - l + 1];        s1 = l;        s2 = m + 1;        int index = 0;        while (s1 <= m && s2 <= r) {            if (a[s1] < a[s2]) {                help[index++] = a[s2++];            } else if (a[s1] > a[s2]) {                help[index++] = a[s1++];            } else {                help[index++] = a[s2++];            }        }        while (s1 <= m) {            help[index++] = a[s1++];        }        while (s2 <= r) {            help[index++] = a[s2++];        }        index = 0;        for (int n : help) {            a[l + (index++)] = n;        }        return ans;    }}

区间和的个数问题

题目描述见：LeetCode 327. Count of Range Sum

本题有几个优化点：

1. 由于需要快速得到区间和，所以，可以通过前缀和数组来加速区间和的求法。

2. 在merge过程中，由于存在单调性，所以可以通过滑动窗口的方式，定位到区间和的上下界，整个过程不回退，所以不会增加归并排序的整体时间复杂度。

完整代码和注释见

class Solution {    public static int countRangeSum(int[] nums, int lower, int upper) {        int size = nums.length;        // 前缀和数组加速求区间的和！！        long[] preSum = new long[size];        preSum[0] = nums[0];        for (int i = 1; i < size; i++) {            preSum[i] = nums[i] + preSum[i - 1];        }        return p(preSum, 0, size - 1, lower, upper);    }    public static int p(long[] preSum, int i, int j, int lower, int upper) {        if (i == j) {            if (preSum[i] >= lower && preSum[j] <= upper) {                return 1;            }            return 0;        }        int mid = i + ((j - i) >> 1);        return p(preSum, i, mid, lower, upper) + p(preSum, mid + 1, j, lower, upper) + merge(preSum, i, mid, j, lower, upper);    }    private static int merge(long[] preSum, int i, int mid, int j, int lower, int upper) {        // 单调性->滑动窗口        int pair = 0;        int L = i;        int R = i;        int S = mid + 1;        // 区间和存在单调性，使用滑动窗口定位上下界，不回退，所以O(logN)        while (S <= j) {            long max = preSum[S] - lower;            long min = preSum[S] - upper;            while (L <= mid && preSum[L] < min) {                L++;            }            while (R <= mid && preSum[R] <= max) {                R++;            }            pair += (R - L);            S++;        }        // mergeSort经典代码        long[] helper = new long[j - i + 1];        int l = i;        int r = mid + 1;        int index = 0;        while (l <= mid && r <= j) {            if (preSum[l] > preSum[r]) {                helper[index++] = preSum[r++];            } else {                helper[index++] = preSum[l++];            }        }        while (l <= mid) {            helper[index++] = preSum[l++];        }        while (r <= j) {            helper[index++] = preSum[r++];        }        int k = 0;        for (long num : helper) {            preSum[i + (k++)] = num;        }        return pair;    }}

更多

算法和数据结构笔记

参考资料

算法和数据结构体系班-左程云